本文主要对AVL树的进行学习总结,并使用C++代码来实现和测试。首先,介绍了AVL树的基本概念和性质。之后,采用图示和代码相结合的方式,重点讲解AVL树如何通过四种旋转方式来保持树的平衡。此外,通过与一般的平衡二叉搜索树进行对比,给出了正常插入,查找和删除三种操作在实现上应当增加的内容。
1.AVL树的概念
AVL树 (Adelson-Velsky and Landis Tree) 是计算机科学中最早被发明的自平衡二叉查找树。AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。AVL树也可以称之为平衡二叉搜索树,简称平衡二叉树。
一个AVL树一定具有如下两个性质:
- 一定是一个二叉搜索树
- 每个节点的左子树和右子树的高度差至多为1
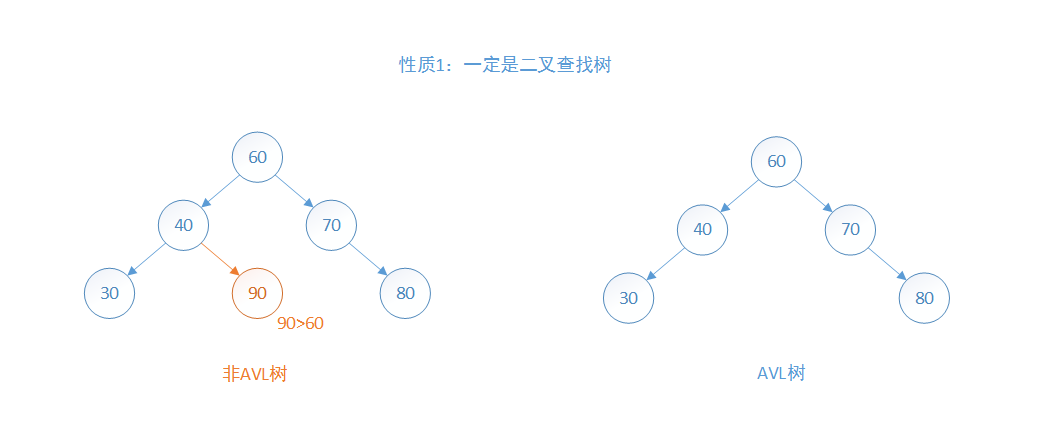
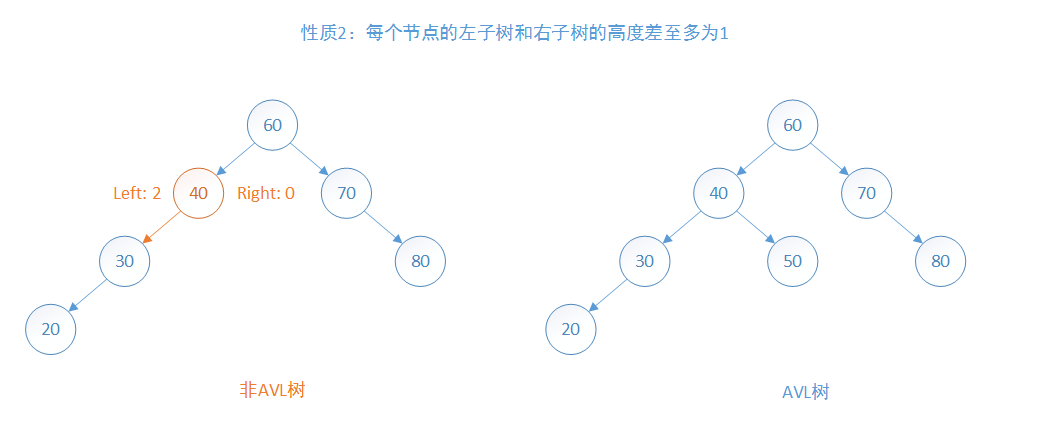
因为树的高度是平衡的,避免了一般二叉搜索树退化成链表的情况,所以AVL树的查找、插入和删除在平均和最坏情况下的时间复杂度都是$O(logn)$。
在插入和删除操作之后,树的高度会发生变化,因而平衡性可能会被打破,这时需要借由一次或多次树旋转,以实现树的重新平衡。在AVL树中,如何进行平衡操作,就是其中重中之重。
2.AVL树的实现
2.1 节点结构
在节点结构上,AVL树增加了height的属性,表示各节点具有的高度。这里节点的初始高度为1,主要是因为创建的节点一开始均为叶子节点,而叶子节点的高度就是1。
template <class K, class V>
class Node {
public:
K key;
V value;
Node<K, V>* left;
Node<K, V>* right;
int height;
Node(K key_, V value_)
{
key = key_;
value = value_;
left = nullptr;
right = nullptr;
height = 1;
}
};
2.2 基本接口
AVL树的基本接口增加了平衡操作,主要通过四种旋转来实现,包括两种单旋转和两种双旋转。
template <class K, class V>
class AVLTree {
··· 已省略部分接口
//根节点
Node<K, V>* root;
//单旋转
Node<K, V>* LL_rotate(Node<K, V>* p);
Node<K, V>* RR_rotate(Node<K, V>* p);
//双旋转
Node<K, V>* RL_rotate(Node<K, V>* p);
Node<K, V>* LR_rotate(Node<K, V>* p);
//获取高度
int get_height(Node<K, V>* p);
//获取节点的平衡因子
int get_balance_factor(Node<K, V>* p);
//平衡节点 (平衡二叉树的关键)
Node<K, V>* balance(Node<K, V>* p);
//插入,查找,删除
Node<K, V>* insert(Node<K, V>* p, K key, V value);
Node<K, V>* find(Node<K, V>* p, K key);
Node<K, V>* remove(Node<K, V>* p, K key);
//返回最大节点和最小节点,用于找前继节点和后继节点
Node<K, V>* find_max(Node<K, V>* p);
Node<K, V>* find_min(Node<K, V>* p);
};
2.3 节点高度
AVL树中的节点的高度就等于其左孩子和右孩子树高的最大值加1。
对于节点P的高度就是:
p->height = max(get_height(p->left), get_height(p->right)) + 1;
其中get_height()是用来获取节点高度。没有直接使用p->height的原因是针对null节点没有height属性的情况,令其直接返回为0。
template <class K, class V>
int AVLTree<K, V>::get_height(Node<K, V>* p)
{
if (p == nullptr)
return 0;
return p->height;
}
所以,如果节点是叶子节点,那么由于null节点高度视为0,计算后的叶子节点高度就为1。因而在创建节点时,节点高度可以初始化为1。
2.4 四种旋转
在介绍旋转之前,对AVL树的插入和删除操作再次明确几个概念:
- 对于插入操作:
- 插入数据一定是在叶子节点上
- 插入数据之前,AVL树一定是满足平衡条件的
- 插入数据之后,AVL树可能会被打破平衡,这时候就需要对树进行旋转操作来实现重新平衡
- 对于删除操作:
- 删除数据也可以替换为在叶子节点上删除
- 删除数据之前,AVL树一定是满足平衡条件的
- 删除数据之后,同样可能会打破AVL树的平衡,这时候也需要对树进行旋转操作实现重新平衡
根据打破平衡情况的不同,可以将场景罗列成四种。针对四种情况,将会有四种旋转方式。
为了便于介绍,旋转将借用图来表示,这里先对图中节点给出定义:
- P : parent 节点。同时, PL 表示 P 节点的左子树, PR 表示 P 节点的右子树。
- C : child 节点。同时, CL 表示 C 节点的左子树, CR 表示 C 节点的右子树。
- CC: child 的 child 节点。同时, CCL 表示 CC 节点的左子树, CCR 表示 CC 节点的右子树。
在图示中,只画出了插入节点后,打破平衡的情况。而对于删除操作,可以理解成另一边的子树,减去了一个节点,同样类似插入节点失去平衡的情况,这里可以自行想象。
LL型 - 右单旋转
如果P的左子树高度为h+1,右子树高度为h。这时候,要是在P的左(L)孩子C的左(L)子树CL上插入新节点,那么P的左子树会变为h+2,而右子树为h,左右子树高度差从1变为2,于是P节点失去平衡。
因为P节点的左子树偏高,这时候可以向右旋转,来重新达到子树平衡:
- 将节点P的左孩子节点C提升为新的子树根节点
- 将原来子树根节点P降为C的右孩子
- 将原来C的右子树CR更换为P的左子树
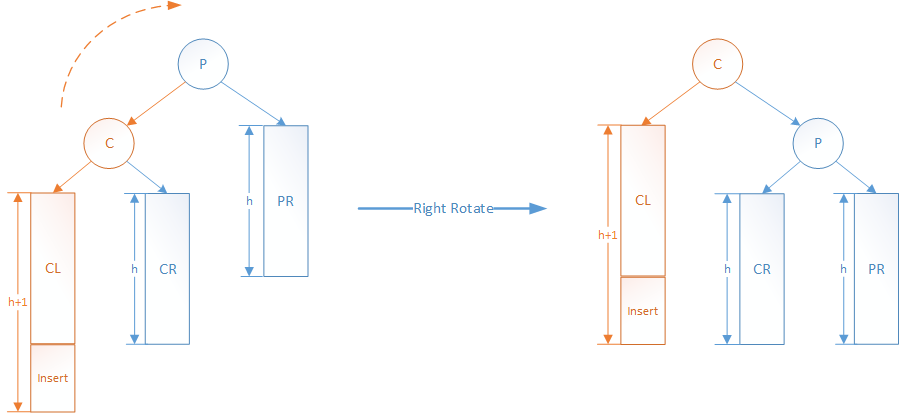
实现上,由于指针赋值关系,实际指针赋值顺序正好与前面陈述旋转的顺序相反。同时,在更新时候也要更新相应节点的高度。
//向右旋转
template <class K, class V>
Node<K, V>* AVLTree<K, V>::rotate_right(Node<K, V>* p)
{
//根节点为P,左孩子为C
Node<K, V>* c = p->left;
//先将C的右子树CR更换为P的左子树
p->left = c->right;
//再将P降为C的右孩子
c->right = p;
//更新P和C的树高
p->height = max(get_height(p->left), get_height(p->right)) + 1;
c->height = max(get_height(c->left), p->height) + 1;
//最后返回C作为新的子树根节点
return c;
}
//LL型 (向右单旋转):因为左孩子C的左子树CL插入节点导致了不平衡
template <class K, class V>
Node<K, V>* AVLTree<K, V>::LL_rotate(Node<K, V>* p)
{
return rotate_right(p);
}
RR型 - 左单旋转
如果P的左子树高度为h,右子树高度为h+1。这时候,要是在P的右(R)孩子C的右(R)子树CR上插入新节点,那么P的右子树会变为h+2,而左子树为h,左右子树高度差从-1变为-2,同样,P节点失去平衡。
因为P节点的右子树偏高,这时候可以向左旋转,来重新达到子树平衡:
- 将节点P的右孩子节点C提升为新的子树根节点
- 将原来子树根节点P降为C的左孩子
- 将原来C的左子树CL更换为P的右子树
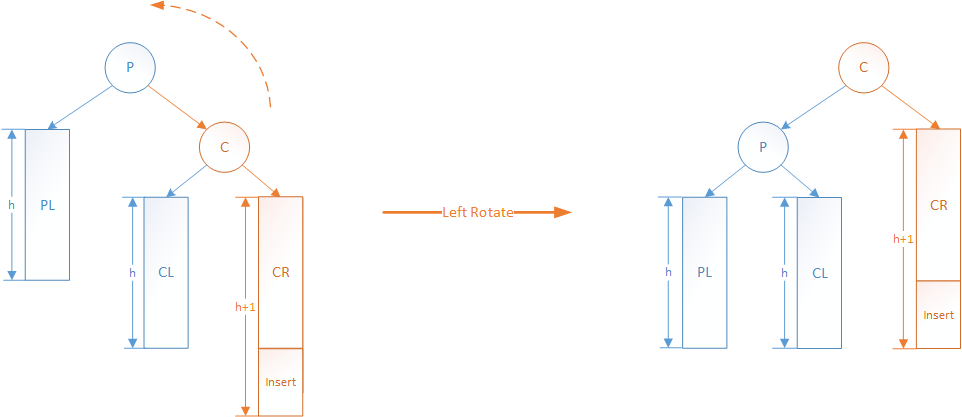
与右单旋转一样,由于指针赋值关系,实际指针赋值顺序正好与前面陈述旋转的顺序相反。同时,在更新时候也要更新相应节点的高度。
//向左旋转
template <class K, class V>
Node<K, V>* AVLTree<K, V>::rotate_left(Node<K, V>* p)
{
//根节点为P,右孩子为C
Node<K, V>* c = p->right;
//先将C的左子树CL更换为P的右子树
p->right = c->left;
//再将P更新为C的右子树
c->left = p;
//更新P和C的树高
p->height = max(get_height(p->left), get_height(p->right)) + 1;
c->height = max(get_height(c->right), p->height) + 1;
//最后返回C作为新的子树根节点
return c;
}
//RR型 (向左单旋转) 因为右孩子C的右子树CR插入节点导致了不平衡
template <class K, class V>
Node<K, V>* AVLTree<K, V>::RR_rotate(Node<K, V>* p)
{
return rotate_left(p);
}
LR型 - 先左后右双旋转
如果P的左子树高度为h+1,右子树高度为h。这时候,要是在P的左(L)孩子C的右(R)孩子CC为根节点的子树上插入新节点,在CC的左子树CCL或者右子树CCR插入均可。那么P的左子树会变为h+2,而右子树为h,左右子树高度差从1变为2,于是P节点失去平衡。
如果对LR型只使用左单旋转,图中节点CC会成为P节点的左子树。可以想象到,旋转后新成为根节点的C的右子树高度为h,但是左子树却为h+2(h+CC+P), 这里对LR型通过向左旋转变成了后面的RL型。
其实,可以通过两次旋转,重新达到子树平衡:
- 先以C为子树根节点,向左旋转,使得P子树成为LL型不平衡
- 再以P为子树根节点,向右旋转,新的子树达到平衡
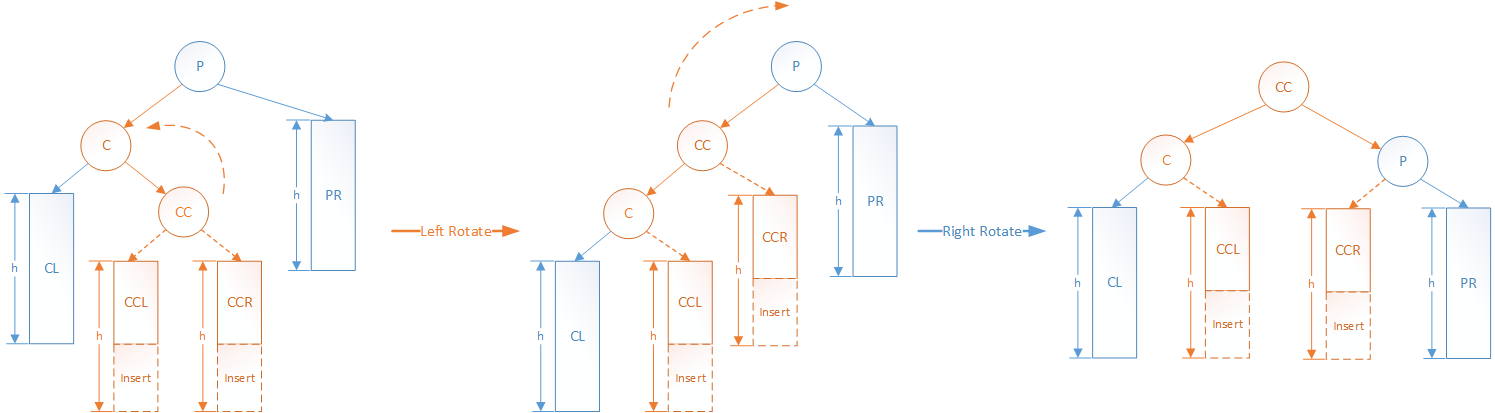
实现上,就是调用两次单旋转。注意要将返回的节点要用于更新新的子树根节点。
//LR型 (先向左后向右双旋转)
template <class K, class V>
Node<K, V>* AVLTree<K, V>::LR_rotate(Node<K, V>* p)
{
p->left = rotate_left(p->left);
return rotate_right(p);
}
RL平衡旋转 - 先右后左双旋转
如果P的左子树高度为h,右子树高度为h+1。这时候,要是在P的右(R)孩子C的左(L)孩子CC为根节点的子树上插入新节点,在CC的左子树CCL或者右子树CCR插入均可。那么P的右子树会变为h+2,而左子树为h,左右子树高度差从-1变为-2,于是P节点失去平衡。
如果对RL型只使用右单旋转,同样,会成为LR型。所以类似的,通过两次旋转,可以使P重新达到平衡:
- 先以C为子树根节点,向右旋转,使得P子树成为RR型不平衡
- 再以P为子树根节点,向左旋转,新的子树达到平衡
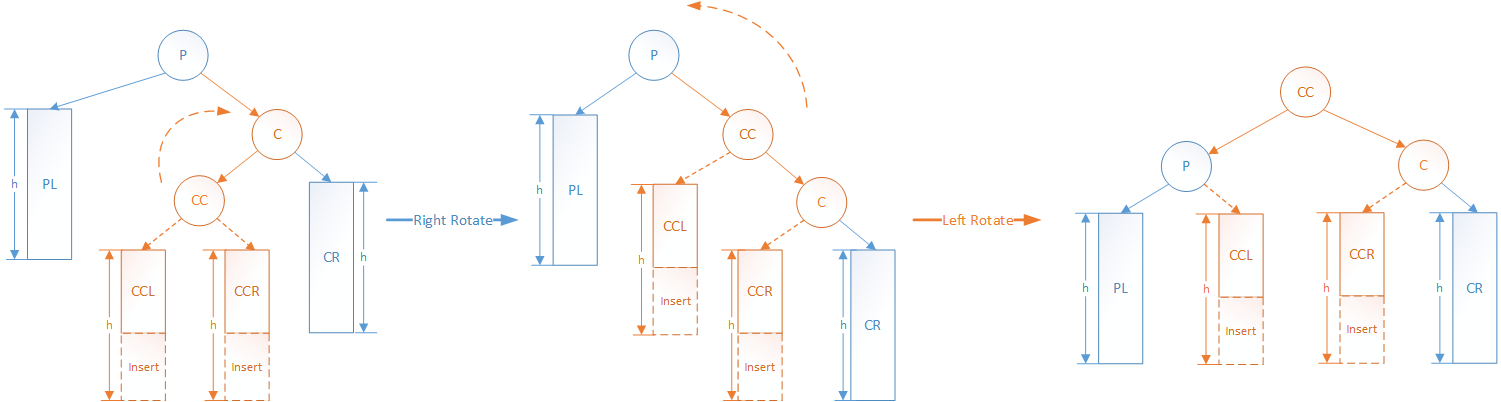
在实现上,与LR是镜像问题,也是调用两次单旋转。这里也可以尝试先调用rotate_left(p)成为LR型,再调用LR_rotate(p)实现平衡。
//RL型(先向右后向左双旋转)
template <class K, class V>
Node<K, V>* AVLTree<K, V>::RL_rotate(Node<K, V>* p)
{
p->right = rotate_right(p->right);
return rotate_left(p);
// 也可以先左旋转换成LR型,再调用LR型旋转
// p = rotate_left(p);
// return LR_rotate(p);
}
2.5 平衡
为了判断AVL树是否平衡,可以通过计算每个节点的平衡因子来确定。
节点p的平衡因子就是其左子树的高度减去其右子树的高度:
template <class K, class V>
int AVLTree<K, V>::get_balance_factor(Node<K, V>* p)
{
return get_height(p->left) - get_height(p->right);
}
如果节点平衡因子大于1或者小于-1,那么就说明该节点为根节点的子树没有达到平衡,这时就需要平衡操作来重新调整。
对于平衡操作,可以通过计算根节点和孩子节点的平衡因子,将不平衡的归类成四种类型,从而调用相应类型的旋转来平衡。
template <class K, class V>
Node<K, V>* AVLTree<K, V>::balance(Node<K, V>* p)
{
//获取根节点的平衡因子
int p_factor = get_balance_factor(p);
//1. 如果左子树树高更高
if (p_factor > 1) {
int c_factor = get_balance_factor(p->left);
if (c_factor > 0) {
//1.1 左子树(L)的左孩子(L)更高
p = LL_rotate(p);
} else {
//1.2 左子树(L)的右孩子(R)更高
p = LR_rotate(p);
}
}
//2. 如果右子树树高更高
if (p_factor < -1) {
int c_factor = get_balance_factor(p->right);
if (c_factor > 0) {
//2.1 右子树(R)的左孩子(L)更高
p = RL_rotate(p);
} else {
//2.2 右子树(R)的右孩子(R)更高
p = RR_rotate(p);
}
}
//返回平衡后的根节点
return p;
}
2.5 插入
相比于一般二叉搜索树,在返回根节点时增加了平衡操作,同时因为插入会改变其他节点高度,需要重新计算一下新的根节点高度。
template <class K, class V>
void AVLTree<K, V>::insert(K key, V value)
{
root = insert(root, key, value);
}
template <class K, class V>
Node<K, V>* AVLTree<K, V>::insert(Node<K, V>* p, K key, V value)
{
//终结条件1: 到达null节点,需新建节点返回,完成插入
if (p == nullptr) {
p = new Node<K, V>(key, value);
return p;
}
//终结条件2:如果key相同,那么只需更新value,这里等同update操作
if (p->key == key) {
p->value = value;
return p;
}
//否则就需要继续寻找子树
if (key < p->key) {
p->left = insert(p->left, key, value);
} else {
p->right = insert(p->right, key, value);
}
//注意:这里相比一般二叉搜索树,在这里增加了平衡语句,这是两者的唯一区别
//因为平衡操作可能导致根节点变化,同样将返回值用于更新根节点返回
p = balance(p);
//插入后还需要更新height
p->height = max(get_height(p->left), get_height(p->right)) + 1;
return p;
}
2.6 查找
查找与一般二叉搜索树相同。
template <class K, class V>
Node<K, V>* AVLTree<K, V>::find(K key)
{
return find(root, key);
}
template <class K, class V>
Node<K, V>* AVLTree<K, V>::find(Node<K, V>* p, K key)
{
//终结条件: 到达null节点,或者找到对应节点
if (p == nullptr || p->key == key) {
return p;
}
//根据二叉搜索树的性质继续寻找
if (key < p->key) {
return find(p->left, key);
} else {
return find(p->right, key);
}
}
2.7 删除
相比于一般二叉搜索树,在返回根节点之前增加了的平衡操作,同时也需要再次更新节点高度。
template <class K, class V>
void AVLTree<K, V>::remove(K key)
{
root = remove(root, key);
}
template <class K, class V>
Node<K, V>* AVLTree<K, V>::remove(Node<K, V>* p, K key)
{
//终结条件1: 到达null节点,仍然没能找到,返回nullptr
if (p == nullptr) {
return p;
}
//终结条件2: 找到删除节点
if (p->key == key) {
//1. 如果没有左右孩子,直接删除该节点
if (p->left == nullptr && p->right == nullptr) {
delete p;
p = nullptr;
return p;
}
//2. 如果只有一个孩子,那么直接将孩子节点作为替换节点, 同时删除节点
if (p->left == nullptr) {
Node<K, V>* replace = p->right;
delete p;
p = nullptr;
return replace;
} else if (p->right == nullptr) {
Node<K, V>* replace = p->left;
delete p;
p = nullptr;
return replace;
}
//3. 剩下就是左右孩子都存在的情况
//注意: 这里与一般二叉搜索树的区别,在于要根据树高选择前驱/后继节点作为替换节点
int p_factor = get_balance_factor(p);
if (p_factor > 0) {
//3.1 左子树更高,则将根节点的值更换为前驱节点
Node<K, V>* replace = find_max(p->left);
p->key = replace->key;
p->value = replace->value;
p->left = remove(p->left, replace->key);
} else {
//3.2 右子树更高, 则将根节点的值更换为后继节点
Node<K, V>* replace = find_min(p->right);
p->key = replace->key;
p->value = replace->value;
p->right = remove(p->right, replace->key);
}
//注意: 这里需要用else if,因为key的值可能会在前面替换节点时被修改了
} else if (key < p->key) {
p->left = remove(p->left, key);
} else {
p->right = remove(p->right, key);
}
//注意: 最后要对节点进行平衡操作
p = balance(p);
//更新height
p->height = max(get_height(p->left), get_height(p->right)) + 1;
return p;
}
3.最后
3.1 完整代码与测试
cpp文件:avl_tree_improve.cpp
运行结果,括号里表示节点高度:
After insert 10, 40, 30, 60, 90, 70, 20, 50, 80:
Pre order traverse: 60(4) 30(3) 10(2) 20(1) 40(2) 50(1) 80(2) 70(1) 90(1)
Mid order traverse: 10(2) 20(1) 30(3) 40(2) 50(1) 60(4) 70(1) 80(2) 90(1)
*************************************
Remove 80 tree balance check: 1
Remove 10 tree balance check: 1
Remove 50 tree balance check: 1
Remove 40 tree balance check: 1
*************************************
After remove 80, 10, 50, 40:
Pre order traverse: 60(3) 30(2) 20(1) 90(2) 70(1)
Mid order traverse: 20(1) 30(2) 60(3) 70(1) 90(2)
3.2 参考文档
-
Wiki - AVL树: https://zh.wikipedia.org/wiki/AVL%E6%A0%91
-
平衡二叉树(AVL)原理解析与实现(C++): https://juejin.cn/post/6844904006033080333
