本文主要总结了二叉搜索树的基本概念和性质,并使用C++实现了具有插入,查找和删除功能的二叉搜索树。其中,在节点结构上考虑了键值两个属性,类型上采用模板编程。基于二叉搜索树的特性,在三种基本操作的实现上,使用了的二分策略和递归遍历的方式。特别的,在删除操作上,还利用了替换叶子节点到删除节点的技巧。
前言
前面介绍了 二叉堆 实际上是一种特殊的完全二叉树,通过利用完全二叉树的特性,使用了数组结构实现了二叉树,并具基于堆有序的性质。那么基于二叉树还有什么其他的数据结构呢?
其实基于二叉的结构性质,很容易想到二分法。那么是不是能够实现一种数据结构,既能使用二叉树的结构来保存数据,同时又能达到对数级别的搜索复杂度呢?可以的,这就是二叉搜索树。
基本概念
二叉搜索树(BST, Binary Search Tree) 在二叉树的基础上,还要具有这条的重要性质:对于任意节点,其左子树的节点的值都比该节点小, 而右子树的节点的值都比该节点大。
比如下面的二叉树(节点集={1,2,3,4,5,6,7})就是组成了一个二叉搜索树。
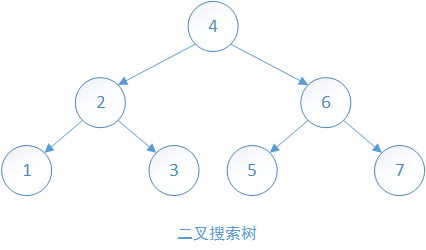
从图中可以发现两点:
-
如果对二叉搜索树进行中序遍历,得到{1,2,3,4,5,6,7},发现是有序的。这正是二叉搜索树的性质决定的。可以通过中序遍历是否有序来判断二叉树是不是二叉搜索树,当然也可以基于性质递归判断。
-
如果对二叉搜索树进行前序遍历,得到{4,2,6,1,3,5,7}。在构造二叉树的时候,可以按照这个顺序依次插入每个节点就能得到同样的二叉搜索树。
基本操作
对二叉搜索树的基本操作包括:插入,查询, 删除。因为二叉树的结构性质,三种操作时间复杂度的最佳情况是 $O(logn)$,而最坏情况是 $O(n)$。
出现最坏情况的原因是,比方同样对于节点集={1,2,3,4,5,6,7}。如果按照这个顺序插入,那么二叉树将退化成为链表,时间复杂度自然退化为 $O(n)$。
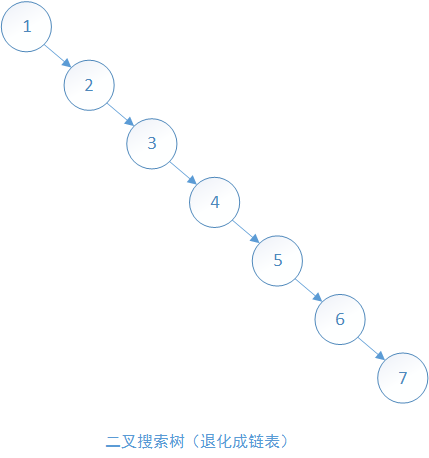
为了保证二叉搜索树操作的时间复杂度稳定为 $O(logn)$,那么就需要一些额外的平衡操作来避免树退化成链表,这就有一些自平衡搜索树出现了,比如AVL树,红黑树。后面将会介绍这些树是如何通过平衡操作,来达到二叉搜索树的自平衡的。
实现
节点结构
节点结构上主要包括两部分,数据部分的键key和值value,指针部分的左指针left和右指针right。比较是通过key来比较,找到对应的key后,就可以返回其key对应的value。
template <class K, class V>
class Node {
public:
K key;
V value;
Node<K, V>* left;
Node<K, V>* right;
Node(K key_, V value_)
{
key = key_;
value = value_;
left = nullptr;
right = nullptr;
}
};
这里节点结构只包含了左右子树两个指针,因为两个指针就足够使用递归方式实现二叉搜索树。在递归返回的时候,会再对父节点进行更新操作,从而避免再去增加一个parent指针。
如果是使用迭代方式实现,则需要在遍历过程中记录父节点,可以通过增加一个局部parent指针方式,或者在节点结构中增加一个parent指针。如果在节点结构中增加一个parent指针,需要增加维护这个parent指针的成本,这时候在树结构改变时一定要加倍注意。
迭代的方式的代码可能没有递归方式的简洁,但可以作为后面的任务,考虑再实现一个迭代方式的一般二叉平衡搜索树。
插入
插入操作就是找到合适的位置,将节点插入。
这里基于二分操作,比较节点key和实际要插入的key:
- 如果是节点key小于要插入的key,那么就在节点的右子树中继续寻找位置
- 如果是节点key大于要插入的key,那么就在节点的右子树中继续寻找位置
通过递归,重复以上比较,直到到达一个合适的位置,满足以下任意条件便可以终止递归:
- 找到的节点为null,那么就可以新建一个节点,将要插入的key和value赋值到该新建节点,并返回
- 找到节点的key 和要插入的key相同,只用更新该节点的value值,并返回
注意: 到达合适位置,最后一定要返回插入后的节点,这样父节点也可以通过p->left or right = insert(p->left or right, key, value) 来更新插入后的左右子树。
template <class K, class V>
void BSTree<K, V>::insert(K key, V value)
{
//注意: 这里要更新root节点
root = insert(root, key, value);
}
template <class K, class V>
Node<K, V>* BSTree<K, V>::insert(Node<K, V>* p, K key, V value)
{
//终结条件1: 到达null节点,需新建节点返回,完成插入
if (p == nullptr) {
p = new Node<K, V>(key, value);
return p;
}
//终结条件2:如果key相同,那么只需更新value,这里等同update操作
if (p->key == key) {
p->value = value;
return p;
}
//否则就需要继续寻找子树
//注意: 这里使用的技巧,将递归返回的节点用于更新左右子树的值,从而实现递归构造树
if (key < p->key) {
p->left = insert(p->left, key, value);
} else {
p->right = insert(p->right, key, value);
}
return p;
}
查询
查询操作就是简单的二分遍历二叉树了。直到找到对应的key或者到达null节点,就可以返回查找到的结果了。
template <class K, class V>
Node<K, V>* BSTree<K, V>::find(K key)
{
return find(root, key);
}
template <class K, class V>
Node<K, V>* BSTree<K, V>::find(Node<K, V>* p, K key)
{
//终结条件: 到达null节点,或者找到对应节点
if (p == nullptr || p->key == key) {
return p;
}
//根据二叉搜索树的性质继续寻找
if (key < p->key) {
return find(p->left, key);
} else {
return find(p->right, key);
}
}
删除
对于删除操作,首先需要通过前面列举的二分递归法,找到需要被删除的节点即找到一个节点的key与要删除的key相同。
找到删除节点后,根据删除节点是否具有左右孩子,还需要分三种情况来处理:
- 如果没有孩子节点,那么就直接删除该节点
- 如果只有左子树,或者只有右子树,那么直接删除该节点,并将子树的根节点返回
- 如果既有左子树,又有右子树,那么可以寻找删除节点的前驱/后继节点作为替代节点,将替换节点直接赋值到删除节点(此时,二叉搜索树有两个相同的节点,均为替换节点)。之后,再利用继续利用二分递归找到重复的替换节点的位置,再进行删除替换节点即可。
注意: 对于插入来说,插入就是插入叶子节点。同样,删除其实也是要删除叶子节点,所以通过找寻替换节点的技巧来轻松实现删除叶子节点。
实际上对于情况2,也可以将子树的根节点只作为替换节点,继续递归删除替换节点,如果替换节点有左右子树就可以转换为情况3,或没有左右子树就转换为情况1,终止递归。但在这里,只用将子树的根节点进行返回就能满足二叉搜索树的性质。不过对其他自平衡二叉搜索树,会考虑将因为删除后需要有相应的平衡操作,所以都替换到叶节点最后删除,将更方便进行的平衡讨论。
删除节点的前驱节点和后继节点的概念:
- 前驱节点即为删除节点的左子树中最大key的节点:以左子树根节点作为起点,不断找该节点的右子树,直到没有右子树的节点即为前驱节点。
- 后继节点即为删除节点的右子树中的最小key的节点:以右子树的根节点作为起点,不断找该节点的左子树,直到没有左子树的节点即为后继节点。
例如,如要找删除节点p的后继节点,将删除节点的右子树的根节点传入下面函数find_min(p->right), 就可以返回删除节点的后继节点。
template <class K, class V>
Node<K, V>* BSTree<K, V>::find_min(Node<K, V>* p)
{
if (p == nullptr)
return p;
while (p->left != nullptr) {
p = p->left;
}
return p;
}
有了找前驱/后继节点的方式,那么删除操作即为:
template <class K, class V>
void BSTree<K, V>::remove(K key)
{
//注意: 这里要更新root节点
root = remove(root, key);
}
template <class K, class V>
Node<K, V>* BSTree<K, V>::remove(Node<K, V>* p, K key)
{
//终结条件1: 到达null节点,仍然没能找到,返回nullptr
if (p == nullptr) {
return p;
}
//终结条件2: 找到删除节点
if (p->key == key) {
//1. 如果没有左右孩子,直接删除该节点
if (p->left == nullptr && p->right == nullptr) {
delete p;
p = nullptr;
return p;
}
//2. 如果只有一个孩子,那么直接将孩子节点作为替换节点, 同时删除节点
// 因为前面已经判断了两个都是nullptr的情况,这里只需判断一个孩子即可
if (p->left == nullptr) {
Node<K, V>* replace = p->right;
delete p;
p = nullptr;
return replace;
} else if (p->right == nullptr) {
Node<K, V>* replace = p->left;
delete p;
p = nullptr;
return replace;
}
//3. 剩下就是左右孩子都存在的情况,这里可以寻找后继节点作为替换节点(也可以使用前驱节点)
Node<K, V>* replace = find_min(p->right);
p->key = replace->key;
p->value = replace->value;
//注意:这里使用的树节点删除技巧,删除节点需要找到一个替代节点,将替代节点放到删除节点位置从而不会破坏树的性质。
//再继续调用同样删除操作去将替换节点删除(更换key值),直到整个树在删除节点后满足基本性质。
if (key > replace->key) {
//key 比 replace 大,说明替换节点在左子树, 这与搜索条件刚好不同, 因为这里搜索的实际是replace->key, key表示的是p->key
p->left = remove(p->left, replace->key);
} else {
p->right = remove(p->right, replace->key);
}
}
//注意: 这里需要用else if,因为key的值可能会在前面替换节点时被修改了
//同时,递归删除树同样需要将返回值用于更新左右子树指针
else if (key < p->key) {
p->left = remove(p->left, key);
} else {
p->right = remove(p->right, key);
}
return p;
}
最后
完整代码链接:
测试结果:
*************************************
After insert 10, 40, 30, 60, 90, 70, 20, 50, 80:
Pre order traverse: 10 40 30 20 60 50 90 70 80
Mid order traverse: 10 20 30 40 50 60 70 80 90
*************************************
After remove 80, 10, 50, 40:
Pre order traverse: 60 30 20 90 70
Mid order traverse: 20 30 60 70 90
这就是关于一般二叉搜索树的实现,总的来说,集中了搜索树的所有基础和关键点,其他的搜索树都是基于这个基本的架构添加更多的概念。通过学习其他的搜索树,返回来再思考最一般的二叉搜索树,一定会有更多的透彻的理解。
