数据结构 红黑树

红黑树

标准模板库中的二叉搜索树

Posted by KunLiu on July 30, 2021

本文继续了二叉搜索树系列，重点学习和总结了红黑树。首先会给出红黑树的定义，然后根据红黑树的性质，解析其在插入和删除操作中如何做到自平衡。最后，也同样提供C++代码实现以供参考。在介绍过程中，也会给出很多值得推敲和思考的点，同时也会不断的与之前的 AVL 树进行对比，从而加深对红黑树的印象。

1. 红黑树的定义

红黑树也是一种自平衡的二叉查找树，相比于 AVL 树，牺牲了部分平衡性，来换取插入/删除后时少量的旋转次数。所以在查找上略慢于 AVL 树，但整体性能要优于 AVL 树。

除了二叉查找树的要求外，红黑树还必须满足以下性质：

  • 性质 1：节点是红色或者黑色。
  • 性质 2：根节点必须是黑色。
  • 性质 3：每个叶子节点（NIL）都是黑色。
  • 性质 4：每一个红色节点的孩子节点一定是黑色的。
  • 性质 5：任意一个节点到其每个叶子节点的所有简单路径都包含相同数目的黑色节点。

由于性质 3，4，可以知道红色节点一定有两个孩子，而且一定是黑色。如果是非叶子的黑色节点, 也一定有两个孩子，但颜色可以是任意的：两个黑，两个红，一个黑一个红。

由于性质 5，如果单看黑色节点，可以知道红黑树具有黑色节点完美平衡的性质。

所以整体来看，红黑树是一个黑色完美平衡的二叉查找树，而红色节点会穿插在两个黑色节点之间。通过这样的性质，保证了从根节点到叶子节点的最长的路径不会是最短的路径的两倍长，使得红黑树在最坏情况下的插入，查找和删除仍然具有对数性能。其中，构成红黑树中最长的路径可能是交替的红色节点和黑色节点，而最短路径可能是全是黑色节点。

下图就是一个红黑树的例子，其中，NIL 为叶子节点。

img1

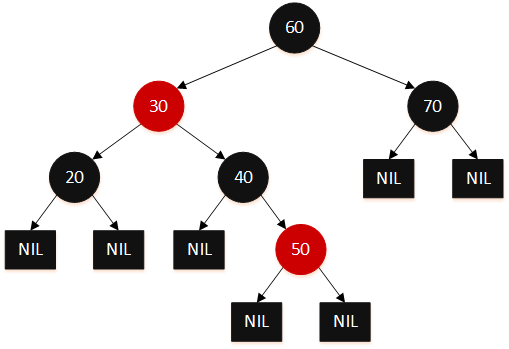
可以看到，首先红黑树是满足了二叉搜索树的性质。对于红色节点 30, 50, 孩子节点均为黑色。而对于黑色节点，孩子可能是一个红一个黑（60, 40），也可能是两个黑（20, 70），当然也有可能接两个红色（插入红色节点 35，会放在 40 的左孩子）。从根节点的最长路径是 60->30->40->50->NIL,而最短路径是 60->70->NIL, 最长路径不超过最短的两倍。所有路径的黑色节点均为 3，整个树是黑色完美平衡的。

2. 红黑树的实现

红黑树可以用类似前面二叉搜索树和 AVL 树的递归方式实现，但网上大多数均以非递归的遍历方式来实现。本文为与前面系列代码结构相统一，依然会以递归实现来讲解。在实际生产应用，也多采用非递归方式，而且会增加一个 parent 指针，来提高整个运行性能。本文最后也同样会给出非递归的实现代码。

2.1 节点结构

在节点结构上，红黑树除了二叉树中基本的left, right 指针，还增加了一个 color 属性, 取值为枚举类型的 RED 或者 BLACK。

enum COLOR { RED, BLACK }

template <class K, class V>
class Node {
public:
    K key;
    V value;
    Node* left;
    Node* right;
    COLOR color;
    Node(K key_, V value_, COLOR color_)
    {
        key = key_;
        value = value_;
        left = nullptr;
        right = nullptr;
        color = color_;
    }
};

大多数红黑树实现过程都会增加 parent 指针，因为存在很多访问父节点的场景。在这里，我们并没有增加 parent指针，这是为减少维护parent的逻辑，专注于红黑树自身算法，但就需要在函数传递过程中，通过参数传入 parent 节点， 甚至是 grandparent 节点。

2.2 基本接口

红黑树也需要旋转来保持平衡，主要是在插入和删除后需要分别进行平衡操作。

template <class K, class V>
class BRTree {

 ··· 已省略部分接口

    //根节点
    Node<K, V>* root;

    //旋转操作
    Node<K, V>* rotate_left(Node<K, V>* p);
    Node<K, V>* rotate_right(Node<K, V>* p);

    //插入
    Node<K, V>* insert(Node<K, V>* p, K key, V value);
    Node<K, V>* insert_balance(Node<K, V>* pp, Node<K, V>* p, Node<K, V>* u);

    //查找
    Node<K, V>* find(Node<K, V>* p, K key);

    //删除
    Node<K, V>* remove(Node<K, V>* p, K key, bool& balance_indicator);
    Node<K, V>* remove_balance(Node<K, V>* p, Node<K, V>* s, bool& balance_indicator);

    //寻找子树最小节点
    Node<K, V>* find_min(Node<K, V>* p);
};

2.3 旋转

红黑树的平衡是主要通过旋转和变色来实现的。旋转分为左旋和右旋，与前面 AVL 树单旋转相同，而变色就是改变节点的color值。

//左旋
template <class K, class V>
Node<K, V>* BRTree<K, V>::rotate_left(Node<K, V>* p)
{
    Node<K, V>* temp = p->right;
    p->right = temp->left;
    temp->left = p;
    return temp;
}

//右旋
template <class K, class V>
Node<K, V>* BRTree<K, V>::rotate_right(Node<K, V>* p)
{
    Node<K, V>* temp = p->left;
    p->left = temp->right;
    temp->right = p;
    return temp;
}

2.4 插入

红黑树的插入操作可以分为寻找插入位置和插入后平衡两个过程。

为了更好的说明插入部分，这里先做出以下节点约定：

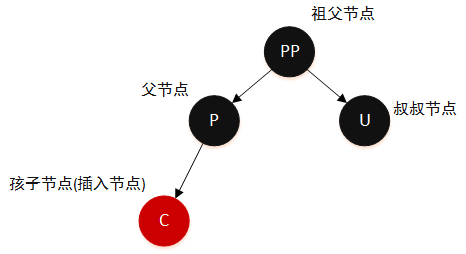
insert-1

  • PP 祖父节点，父节点的父节点
  • P 父节点(Parent)
  • U 叔叔节点(Uncle)，即父节点的兄弟节点
  • C 孩子节点(Children)，这里就表示插入节点

2.4.1 寻找插入位置

对于寻找插入位置来说，与正常二叉搜索树的插入过程基本相同。通过递归遍历红黑树中的节点：

  • 如果节点key小于要插入的key，那么就在节点的右子树中继续寻找位置
  • 如果节点key大于要插入的key，那么就在节点的右子树中继续寻找位置
  • 如果节点为NULL，那么该位置即为插入位置。
  • 如果节点的key和插入的key相同，则只更新节点的value，返回。

红黑树因为节点多了颜色属性，所以有一个问题就是 新插入节点的颜色要设置成什么呢？答案是红色。 如果插入是黑色节点，那么一定会增加该路径的黑色节点数目，破坏了黑色完美平衡的性质，就必须要做平衡操作。而插入红色节点，如果父节点是黑色节点，就不需要做平衡操作了。不过如果插入的是根节点还需要对颜色进行特殊处理，由于红黑树性质 2，根节点是黑色，所以额外把根节点再设为黑色。

//插入
template <class K, class V>
void BRTree<K, V>::insert(K key, V value)
{

    root = insert(root, key, value);
    //注意：保证根节点为黑色
    root->color = BLACK;
}

template <class K, class V>
Node<K, V>* BRTree<K, V>::insert(Node<K, V>* p, K key, V value)
{
    //终结条件1: 到达null节点，需新建节点返回，完成插入
    if (p == nullptr) {
        p = new Node<K, V>(key, value, RED);
        return p;
    }

    //终止条件2: key已经存在并且找到，则直接更新value, 相当于更新操作
    if (p->key == key) {
        p->value = value;
        return p;
    }

    //否则，继续利用递归寻找合适位置插入
    if (key < p->key) {
        p->left = insert(p->left, key, value);
        //插入后，可能需要平衡操作
        p = insert_balance(p, p->left, p->right);
    } else {
        p->right = insert(p->right, key, value);
        p = insert_balance(p, p->right, p->left);
    }
    //返回子树根节点p用于更新
    return p;
}

2.4.2 插入后平衡

插入后什么情况才需要平衡呢？答案一定是破坏了红黑树基本性质的情况下才需要。这里知道除了根节点插入是黑色，其他插入节点将被设为红色，那么有可能破坏的只有性质 4，插入后出现了两个连起来的红色节点。

所以只有当插入节点的父节点为红色，才会需要插入后的平衡操作。

由父节点是红色还能得到什么其他结论呢？ 根据性质 2，根节点为黑色，可以确定插入节点一定有祖父节点，而且根据性质 4，祖父节点一定是黑色的。这一点很重要，因为插入后的平衡需要有祖父节点的参与，确定存在祖父节点和颜色可以减少很多判断。

当插入后的平衡被打破后，要如何让红黑树重新平衡呢？这里可以先将打破平衡后的情景分一下，再根据不同情景进行不同的恢复平衡操作：

  • 情景 1：叔叔节点存在，并且为红色节点
  • 情景 2：叔叔节点不存在，或者为黑色节点
    • 情景 2.1：父节点是祖父结点的左孩子，插入节点是父结点的左孩子 (L-L 型)
    • 情景 2.2：父节点是祖父结点的左孩子，插入节点是父结点的右孩子 (L-R 型)
    • 情景 2.3：父节点是祖父结点的右孩子，插入节点是父结点的左孩子 (R-L 型)
    • 情景 2.4：父节点是祖父结点的右孩子，插入节点是父结点的左孩子 (R-L 型)

下面对各个情景，逐个分析：

情景 1：叔叔节点存在并且为红节点

在这种情景下，由于父节点和叔叔节点同时为红色，前面根据红黑树性质已经推断出了祖父节点一定为黑色。在这里只需要变色操作，将“黑红红” 变成 “红黑红”，则至少将这部分子树变成黑色平衡。

所以处理过程：

  • 将P和U设置为黑色
  • 将PP设置为红色
  • 把PP设置为插入结点, 继续向上回溯

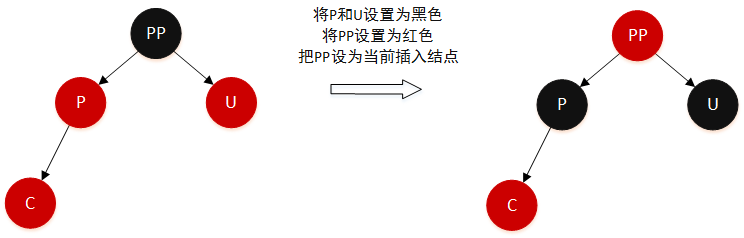
insert-balance-1

由于PP变成了红色，，如果PP的父节点是黑色，那么无需再做额外的平衡了。但如果PP的父节点是红色，就还需要把PP当作新的插入结点，继续做插入后的平衡操作，直到整个红黑树平衡为止。

那么如果PP刚好为根节点，或者回溯过程中新的PP节点为根节点，那么根据性质 2，就必须把PP设置为黑色，该子树的红黑结构变为了 “黑黑红”。这样，从根节点到叶子节点的路径中，黑色节点数目增加了。这也是唯一一种会增加红黑树黑色节点层数的插入情景。

你可能会想，为什么不一开始就把“黑红红” 变成 “黑黑红”？ 这样是不行的，因为该子树本来的黑色节点个数为 1，而变色后，黑色节点个数变成了 2，相比于其他子树，一定会打破性质 5，根节点到各个叶子的路径中黑色个数均相同。 而只有当回溯到了根节点，只将根节点从红色变成黑色是不会打破这个黑色个数平衡的。你学到了吗？

情景 2：叔叔节点不存在，或者为黑色节点

由于叔叔节点不存在（其实为黑色的 NIL 节点），或者为黑色节点，如果单纯的对叔叔变色必然会导致叔叔节点的路径的黑色节点数目减少。所以这里就需要旋转的操作来将两个红色节点，移到祖父节点的两边，即分给叔叔节点那边路径一个红色，在祖父和叔叔中间插入，不就又平衡了嘛。

这里又可以根据父节点和孩子节点的位置分四种情景来平衡：

情景 2.1：父节点是祖父结点的左孩子，插入节点是父结点的左孩子 (L-L 型)

通过右旋将祖父节点移到右分支，然后再处理颜色使子树达到平衡即可：

  • 对PP进行右旋
  • 将P设为黑色
  • 将PP设为红色

insert-balance-2

这样在旋转变色后，子树达到平衡的同时，整个树也同样达到了平衡。注意在实现上，这里的P在旋转后，会变成新的祖父节点，而PP节点成为了P右孩子。

这里如果在变色时，将C和PP设置为黑色，P设置为红色，再作为P作为新的插入节点是不是也可以。当然可以，但是这样就得像情景 1 中，不断的向上回溯判断，反而增加了平衡的复杂度。

情景 2.2：父节点是祖父结点的左孩子，插入节点是父结点的右孩子 (L-R 型)

这种情景可以先通过以父节点为根节点，进行左旋，即可转换成情景 2.1 所以处理过程：

  • 对P进行左旋
  • 得到情景 2.1
  • 按照情景 2.1 处理

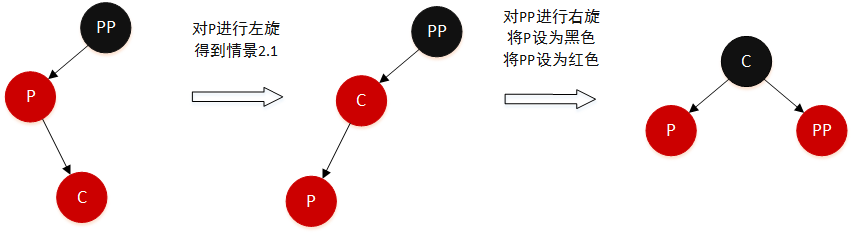
insert-balance-3

这里如果不先以P左旋，按照情景 2.1，先直接以PP右旋，虽然旋转后的颜色将变成“红黑红”，但在黑色节点的数目上会导致右子树比左子树多一，仍然处于不平衡状态。还是要通过一定的旋转变色达到根为黑，两边个一个红色的状态。

情景 2.3：父节点是祖父结点的右孩子，插入节点是父结点的左孩子 (R-L 型)

这种情景就是情景 2.1 的镜像，直接左旋变色处理：

  • 对PP进行左旋
  • 将P设为黑色
  • 将PP设为红色

insert-balance-4

同样在实现上注意新的祖父节点换成了P节点, PP节点是P左孩子。

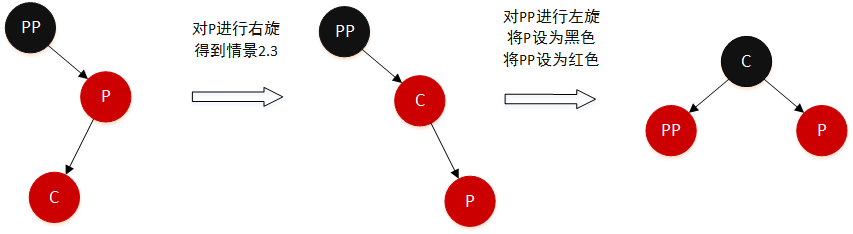
情景 2.4：父节点是祖父结点的右孩子，插入节点是父结点的左孩子 (R-L 型)

同样是情景 2.2 的镜像，先右旋成为情景 2.3 再处理：

  • 对P进行右旋
  • 得到情景 2.3
  • 按照情景 2.3 处理

insert-balance-5

插入平衡的代码实现

好了，分析了这么多，插入后的平衡在实现上就需要区分一下各个情景，然后调用相应的旋转和变色。

// pp: grandparent 祖父节点
// p : parent 父节点
// c : child 孩子节点
// u : uncle 叔叔节点
template <class K, class V>
Node<K, V>* BRTree<K, V>::insert_balance(Node<K, V>* pp, Node<K, V>* p, Node<K, V>* u)
{
    //判断是否有红色节点的儿子
    Node<K, V>* c = nullptr;
    if (p->left != nullptr && p->left->color == RED) {
        c = p->left;
    } else if (p->right != nullptr && p->right->color == RED) {
        c = p->right;
    }

    //平衡条件：插入结点的父结点为红节点, 同时存在也为红色节点的儿子
    if (p->color == RED && c != nullptr) {

        //情景1：叔叔结点存在并且为红结点
        if (u != nullptr && u->color == RED) {
            //变色完再将pp作为插入节点返回
            u->color = BLACK;
            p->color = BLACK;
            pp->color = RED;
            return pp;
        }

        //情景2: 叔叔节点不存在或者为黑色节点
        if (p == pp->left) {
            //情景2.2: 父节点是祖父节点的左孩子， 插入结点是其父节点的右儿子 （L-R型）
            if (c == p->right) {
                //先以p进行左旋，使之成为2.1场景
                p = rotate_left(p);
                pp->left = p;
            }

            //情景2.1: 父节点是祖父节点的左孩子，插入结点是其父节点的左儿子 （L-L型）
            pp = rotate_right(pp);
            //变色
            pp->color = BLACK;
            pp->right->color = RED;

        } else {
            //情景2.4: 如果父节点是祖父节点的右孩子, 插入结点是其父节点的左儿子 （R-L型）
            if (c == p->left) {
                //先进行右旋，使之成为2.3场景
                p = rotate_right(p);
                pp->right = p;
            }

            //情景2.3: 如果父节点是祖父节点的右孩子, 插入结点是其父节点的右儿子 （R-R型）
            pp = rotate_left(pp);
            //变色
            pp->color = BLACK;
            pp->left->color = RED;
        }
    }
    return pp;
}

2.4.3 插入总结

这里再将红黑树的插入与 AVL 树进行一下对比，加深一下印象，如果没有学习 AVL 树，可以先跳过这部分，并不会有任何影响。

首先，在寻找插入位置时，两者逻辑并没有区别。只不过由于 AVL 树更为严格（树高差最大为 1），所以总概率来看寻找插入位置应该更快。两者的主要区别在插入后如何平衡上，但平衡上也有相应的相通之处。

在平衡判断上，两者都是因为树的平衡性质被打破导致。对于 AVL 树，就是插入位置导致子树间高度差增加了。而红黑树则是因为红色节点相连导致，因为这种情景出现的概率相比要小，所以需要旋转次数要更少。

在平衡情景上，AVL 树也同样存在 LL，LR，RL，RR 四种旋转情景，目的也是为了将一个节点从一个子树移到另一边的子树。但红黑树因为多了颜色的属性，所以会增加变色的过程，同时还多出了一个只需要变色就能够实现平衡的情景。

2.5 查找

红黑树的查找逻辑与二叉搜索树是完全一致的。

//查找
template <class K, class V>
Node<K, V>* BRTree<K, V>::find(K key)
{
    return find(root, key);
}

template <class K, class V>
Node<K, V>* BRTree<K, V>::find(Node<K, V>* p, K key)
{
    //终结条件: 到达null节点，或者找到对应节点
    if (p == nullptr || p->key == key) {
        return p;
    }

    //继续寻找
    if (key < p->key) {
        return find(p->left, key);
    } else {
        return find(p->right, key);
    }
}

2.6 删除

对于删除操作同样也可以分为寻找删除位置和删除后平衡两个过程。

为了更好的说明删除部分，这里先做出以下节点约定：

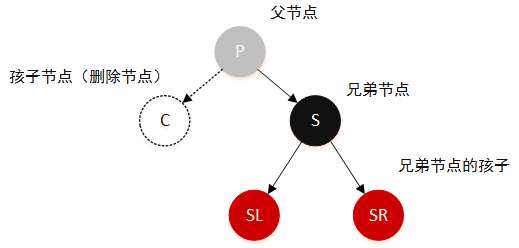
delete-1

  • P 父节点
  • S 兄弟节点 (Sibling)
  • C 孩子节点，这里就表示被删除掉的节点

灰色代表颜色可以是黑色也可以是红色。

相比于插入考虑的节点，这里不需要考虑祖父节点和叔叔节点，但要考虑删除节点的兄弟节点的情况。

2.6.1 寻找删除位置

寻找删除位置同样与二叉搜索树删除基本类似：

  • 如果删除节点没有孩子，就直接删除
  • 如果删除节点只有一个孩子，就用孩子节点替换删除节点
  • 如果删除节点有两个孩子，就用后继节点（也可以用前驱节点）替换删除节点

这里注意替换时候，只需要要将替换节点key的value更新到删除节点，颜色还沿用之前被删除节点的颜色就可以继续维持之前的平衡。然后再以替换节点作为新的删除节点，继续向下寻找。由于不断的替换，最后一定会满足节点没有孩子的条件而被直接删除掉。所以最终的删除节点的位置一定是在树末。所以，在删除节点后平衡考虑，只需要考虑树末节点就可以了。

于是可以写出寻找删除位置的代码：

//删除
template <class K, class V>
void BRTree<K, V>::remove(K key)
{
    bool balance_indicator = false;
    root = remove(root, key, balance_indicator);
}

template <class K, class V>
Node<K, V>* BRTree<K, V>::remove(Node<K, V>* p, K key, bool& balance_indicator)
{
    //终结条件1: 到达null节点，仍然没能找到，返回nullptr
    if (p == nullptr) {
        return p;
    }

    //终结条件2： 找到删除节点
    if (p->key == key) {
        //1. 如果没有左右孩子，直接删除该节点
        if (p->left == nullptr && p->right == nullptr) {

            //如果替换结点是黑结点, 才需要平衡，通过balance_indicator告诉parent节点
            if (p->color == BLACK) {
                balance_indicator = true;
            }
            delete p;
            p = nullptr;
            return p;
        }

        Node<K, V>* replace = nullptr;
        //2. 如果只有一个孩子，就直接将孩子节点作为替换节点
        if (p->left == nullptr) {
            replace = p->right;
        } else if (p->right == nullptr) {
            replace = p->left;
        } else {
            //3. 如果左右孩子都存在，寻找后继节点（也可以使用前驱节点）作为替换节点
            replace = find_min(p->right);
        }

        p->key = replace->key;
        p->value = replace->value;
        //注意：这里使用的树节点删除技巧，删除节点需要找到一个替代节点，将替代节点放到删除节点位置从而不会破坏树的性质。
        //再继续调用同样删除操作去将替换节点删除（更换key值），直到整个树在删除节点后满足基本性质。
        if (key > replace->key) {
            p->left = remove(p->left, replace->key, balance_indicator);
            if (balance_indicator) {
                p = remove_balance(p, p->right, balance_indicator);
            }
        } else {
            p->right = remove(p->right, replace->key, balance_indicator);
            if (balance_indicator) {
                p = remove_balance(p, p->left, balance_indicator);
            }
        }

    }
    //注意： 这里需要用else if，因为key的值可能会在前面替换节点时被修改了
    else if (key < p->key) {
        p->left = remove(p->left, key, balance_indicator);
        if (balance_indicator) {
            p = remove_balance(p, p->right, balance_indicator);
        }

    } else {
        p->right = remove(p->right, key, balance_indicator);
        if (balance_indicator) {
            p = remove_balance(p, p->left, balance_indicator);
        }
    }
    return p;
}

//返回节点p的最左子树节点，用于找到后继节点
template <class K, class V>
Node<K, V>* BRTree<K, V>::find_min(Node<K, V>* p)
{
    if (p == nullptr)
        return p;
    while (p->left != nullptr) {
        p = p->left;
    }
    return p;
}

这里先增加了一个balance_indicator，目的是用于告诉父节点是否需要进行删除后平衡操作。主要因为采用的是递归，同时也没有在节点结构中没有增加parent指针，所以删除节点只能通过一个balance_indicator 在回溯的时候告诉父节点，具体在什么情况下需要进行平衡操作和怎么平衡操作，就在下一节具体讲解。

2.6.2 删除后平衡

删除节点后的平衡操作相比插入平衡要更为复杂，那么先考虑一下删除什么节点会导致红黑树失去平衡呢？如果删除的是红色节点，那么并不会影响到红黑树平衡，所以无需平衡操作。而如果删除的是黑色节点，那么该路径的上黑色节点将减少，红黑树的性质 5 就被打破了，从而不得不需要平衡操作。

所以当删除节点是黑色时，就需要进行平衡操作。

下面就先给出删除节点后的各种情景，从而分析相应的平衡操作：

  • 情景 1： 删除节点是父结点的左孩子
    • 情景 1.1：删除节点的兄弟节点是黑色，兄弟结点的右孩子是红色，左孩子颜色任意
    • 情景 1.2：删除节点的兄弟节点是黑色，兄弟节点的右孩子为黑色，左孩子为红色
    • 情景 1.3：删除节点的兄弟节点是黑色，且兄弟节点的孩子均为黑色 （包括 NIL节点）
    • 情景 1.4：删除节点的兄弟节点是红色
  • 情景 2： 删除节点是父节点的右孩子
    • 情景 2.1：删除节点的兄弟节点是黑色，兄弟结点的左孩子是红色，右孩子颜色任意
    • 情景 2.2：删除节点的兄弟节点是黑色，兄弟节点的左孩子为黑色，右孩子为红色
    • 情景 2.3：删除节点的兄弟节点是黑色，且兄弟节点的孩子均为黑色 （包括 NIL节点）
    • 情景 2.4：删除节点的兄弟节点是红色

情景 1： 删除节点是父结点的左孩子

由于左子树就少了一个黑色节点，在这种情景下, 就需要想办法从别的地方拿一个红色节点吗，然后通过变色来弥补删除的黑色节点。

根据借的方式不同可以分为四种情景讨论，其中三种情景是删除节点的兄弟节点是黑色，一种情景是兄弟节点是红色。如果兄弟节点是黑色，其父节点和孩子节点的具体颜色也无法确定，所以需要根据兄弟节点的孩子节点颜色的不同再分情况讨论。 如果兄弟节点是红色，根据性质 3，其父节点和孩子节点一定都是黑色，只会出现一种情景。

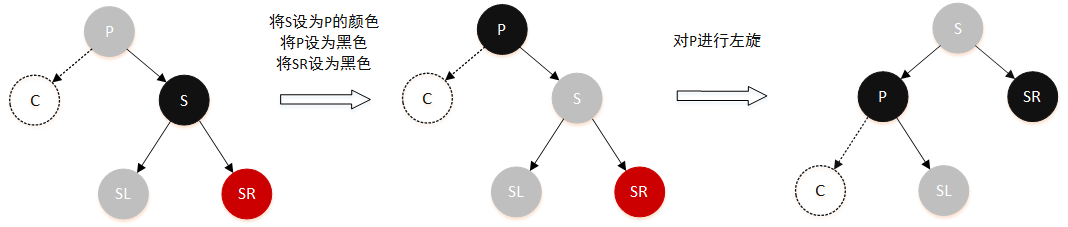
情景 1.1 删除节点的兄弟节点是黑色，兄弟结点的右孩子是红色，左孩子颜色任意

由于兄弟节点的右孩子是红色，这样就可以从右子树拿一个节点到左子树来，变成黑色，就可以完成平衡了。操作就是通过旋转和变色完成：

  • 将S的颜色设为P的颜色
  • 将P设为黑色
  • 将SR设为黑色
  • 对P进行左旋

delete-balance-1

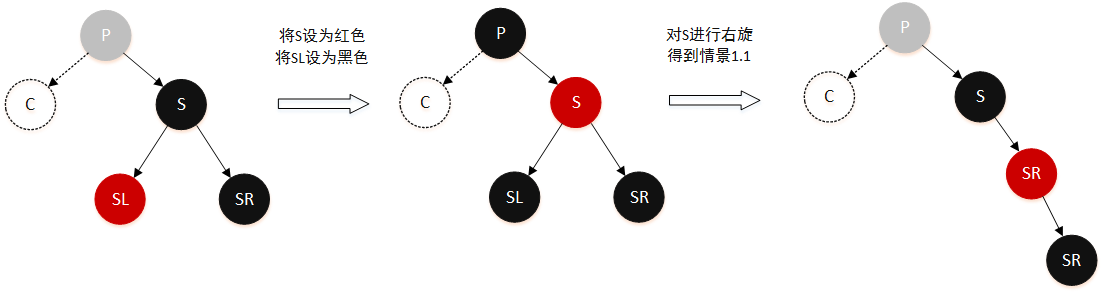
情景 1.2 删除节点的兄弟节点是黑色，兄弟节点的右孩子为黑色，左孩子为红色

由于兄弟节点的左孩子是红色，依然可以从右子树拿一个节点到左子树来，变成黑色来完成平衡。这里先通过旋转把左孩子移到右孩子位置，变成情景 1.1 来统一处理：

  • 将S设为红色
  • 将SL设为黑色
  • 对S进行右旋，得到情景 1.1
  • 按照情景 1.1 处理

delete-balance-2

情景 1.3 删除节点的兄弟节点是黑色，且兄弟节点的孩子均为黑色 （包括 NIL 节点）

由于右子树中的节点都是黑色，没办法借了，那怎么办呢？干脆大家都别过了，都少一个黑色节点算了。但这样的话，子树是黑色平衡的，但相比于其他子树就少了一层黑色节点，就需要告诉其他子树，我们这里少了一个黑色节点，你们有没有办法借一个红色节点给我，不行就一起减去一层黑色。所以，在处理黑色变红色后，要将P作为新的被删除的节点，继续向上判断：

  • 将 S 设为红色
  • 把 P 作为新的删除节点
  • 继续平衡判断

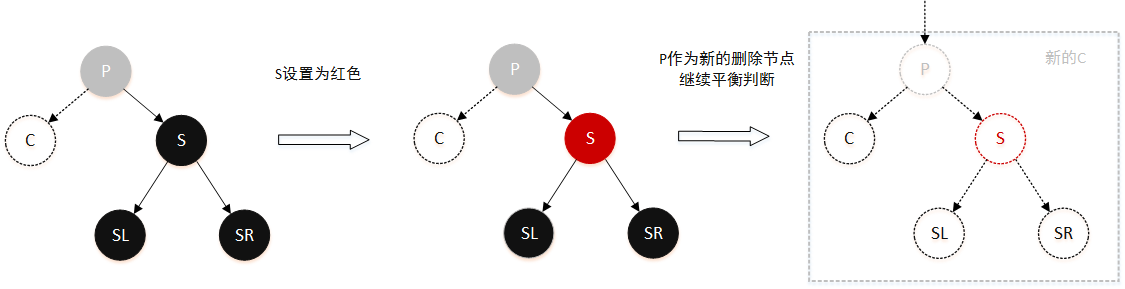
delete-balance-3

你可能在想这两个黑色节点不是一定是 NIL 节点吗？作为一开始确实是的。但是由于会向上遍历，其实删除节点不一定就是删除节点，而可能是被作为删除节点的子树的根节点P, 所以后面不一定就是NIL节点了。

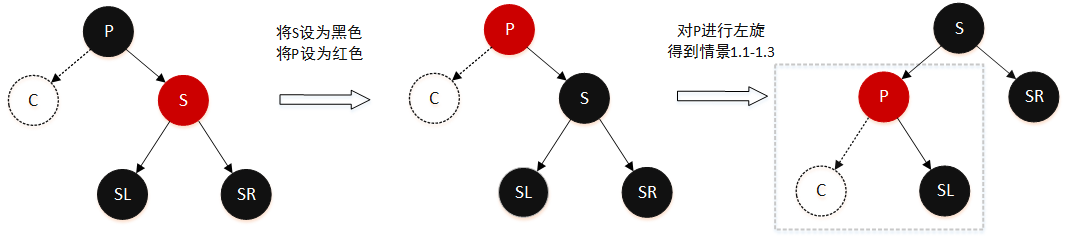
情景 1.4：删除节点的兄弟节点是红色

如果兄弟节点是红色，可以确定其父节点和孩子节点一定是黑色。但借兄弟节点没有借兄弟的孩子容易，因为红色的兄弟节点可能会有两个孩子（非NIL节点）的情况，需要再匀一个黑色孩子过来，成为了删除节点的新的兄弟节点。其左子树需要重新按照情况 1.1-1.3，对左子树判断处理：

  • 将 S 设为黑色
  • 将 P 设为红色
  • 对 P 进行左旋，左子树得到情景 1.1-1.3
  • 左子树按照情景 1.1-1.3 处理

delete-balance-4

情景 2：删除节点是父节点的右孩子

对于情况是右孩子的操作完全是左孩子的镜像。

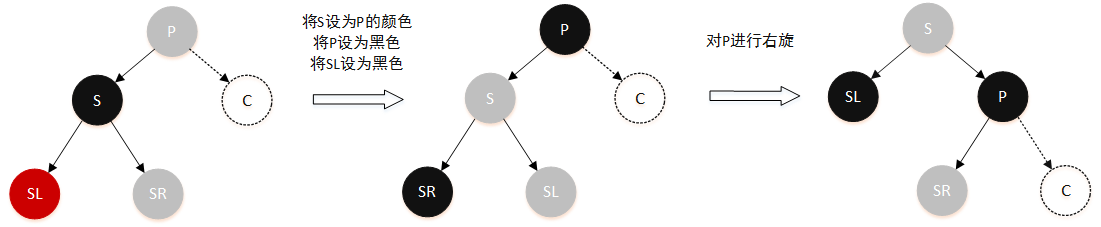
情景 2.1：删除节点的兄弟节点是黑色，兄弟结点的左孩子是红色，右孩子颜色任意 这里就是向左子树来拿一个红色节点过来变成黑色：

  • 将S的颜色设为P的颜色
  • 将P设为黑色
  • 将SL设为黑色
  • 对P进行右旋

delete-balance-5

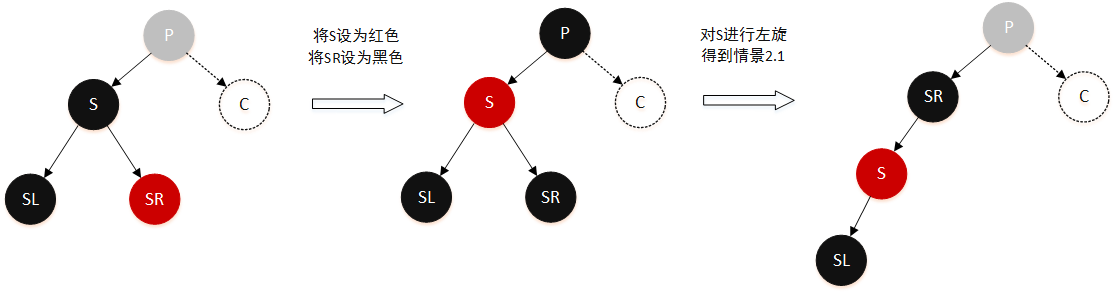
情景 2.2：删除节点的兄弟节点是黑色，兄弟节点的左孩子为黑色，右孩子为红色

同样，先通过旋转变成情景 2.1 再处理：

  • 将S设为红色
  • 将SR设为黑色
  • 对S进行左旋，得到情景 2.1
  • 按照情景 2.1 处理

delete-balance-6

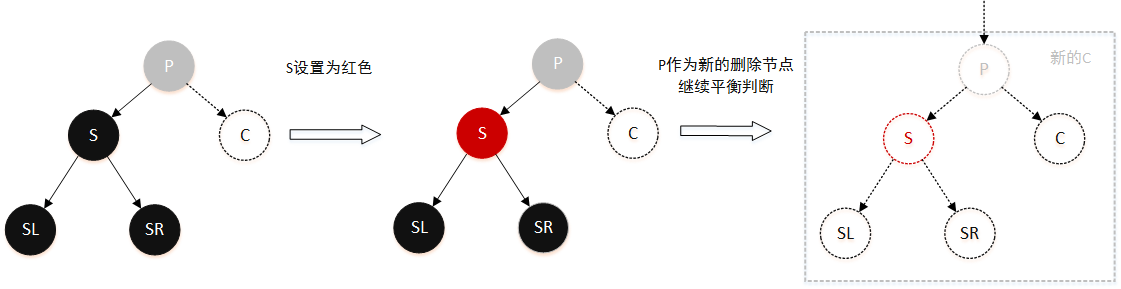
情景 2.3：删除节点的兄弟节点是黑色，且兄弟节点的孩子均为黑色 （包括 NIL节点）

这种情景下就是先变色，再向上询问：

  • 将 S 设为红色
  • 把 P 作为新的删除节点
  • 继续平衡判断

delete-balance-7

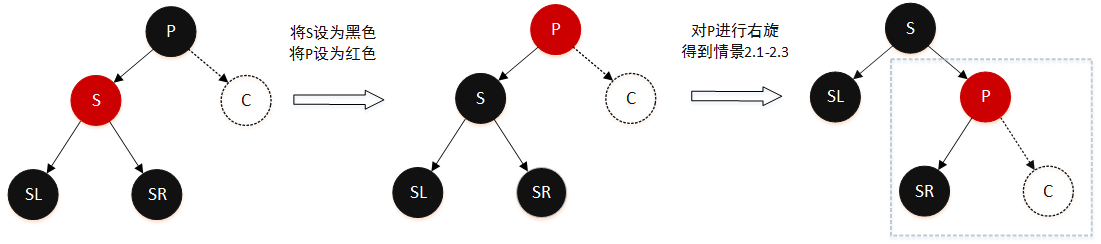
情景 2.4：删除节点的兄弟节点是红色

变色再旋转，处理好右子树：

  • 将 S 设为黑色
  • 将 P 设为红色
  • 对 P 进行右旋，右子树得到情景 2.1-2.3
  • 右子树按照情景 2.1-2.3 处理

delete-balance-8

删除后平衡的代码实现

根据以上情景分析，可以写出对应代码。

//删除平衡
//p: parent 父节点
//s: sibling 兄弟节点
template <class K, class V>
Node<K, V>* BRTree<K, V>::remove_balance(Node<K, V>* p, Node<K, V>* s, bool& balance_indicator)
{

    //情景1：删除节点是父结点的左孩子
    if (p->right == s) {
        //情景1.4：删除节点的兄弟节点是红色
        if (s->color == RED) {
            s->color = BLACK;
            p->color = RED;
            p = rotate_left(p);
            //先调用balance方法处理左子树（情景1.1-1.3）
            if (p->left->right != nullptr) {
                p->left = remove_balance(p->left, p->left->right, balance_indicator);
            }
            s = p->right;
        }
        //情景1.1 - 1.3：删除节点的兄弟节点是黑色
        if (s->color == BLACK) {
            //情景1.3：兄弟节点的孩子均为黑色(包括NIL节点)
            if ((s->left == nullptr || s->left->color == BLACK)
                && (s->right == nullptr || s->right->color == BLACK)) {
                s->color = RED;
                //p 视为新的替换节点, 不改变indicator，返回后继续删除平衡操作
                return p;
            } else {
                //情景1.2：兄弟节点的右孩子为黑色，左孩子为红色
                if ((s->right == nullptr || s->right->color == BLACK)) {
                    s->color = RED;
                    if (s->left != nullptr) {
                        s->left->color = BLACK;
                    }
                    //转换为删除情景1.1
                    s = rotate_right(s); //rotate之后更新新的兄弟节点
                    //注意：这里要将新的s链接上p
                    p->right = s;
                }

                //情景1.1：兄弟结点的右孩子是红色，左孩子颜色任意
                s->color = p->color;
                p->color = BLACK;
                if (s->right != nullptr) {
                    s->right->color = BLACK;
                }
                p = rotate_left(p);
                //平衡indicator 清除
                balance_indicator = false;
                return p;
            }
        }
    } else { //情景2： 删除节点是父节点的右孩子
        //情景2.4：删除节点的兄弟节点是红色
        if (s->color == RED) {
            s->color = BLACK;
            p->color = RED;
            p = rotate_right(p);
            //先调用balance方法处理左子树（情景2.1-2.3）
            if (p->right->left != nullptr) {
                p->right = remove_balance(p->right, p->right->left, balance_indicator);
            }
            s = p->left;
        }
        //情景2.1 - 2.3：删除节点的兄弟节点是黑色
        if (s->color == BLACK) {
            //情景2.3：兄弟节点的孩子均为黑色(包括NIL节点)
            if ((s->left == nullptr || s->left->color == BLACK)
                && (s->right == nullptr || s->right->color == BLACK)) {
                s->color = RED;
                //p 视为新的替换节点, 不改变indicator，返回后继续删除平衡操作
                return p;
            } else {
                //情景2.2：兄弟节点的左孩子为黑色，右孩子为红色
                if ((s->left == nullptr || s->left->color == BLACK)) {
                    s->color = RED;
                    if (s->right != nullptr) {
                        s->right->color = BLACK;
                    }
                    //转换为情景2.1
                    s = rotate_left(s); //rotate之后更新新的兄弟节点
                    //注意：这里要将新的s链接上p
                    p->left = s;
                }

                //情景2.1：兄弟结点的左孩子是红色，右孩子颜色任意
                s->color = p->color;
                p->color = BLACK;
                if (s->left != nullptr) {
                    s->left->color = BLACK;
                }
                p = rotate_right(p);
                //平衡indicator 清除
                balance_indicator = false;
                return p;
            }
        }
    }
}

2.6.3 删除总结

从什么时候需要平衡上，对比红黑树的插入与删除：

  • 插入操作可能产生红色节点相邻的情景，违背了性质 3，所以当插入是红色节点才会打破平衡。
  • 删除操作可能会产生黑色节点减少，违背性质 5，所以当删除的是黑色节点才会打破平衡。

从怎么进行平衡操作上，对比红黑树的插入与删除：

  • 插入平衡主要是看叔叔节点，看能不能帮忙匀走一个红色节点。实在不行，只能通过变色增加一层黑色节点，再向上询问。
  • 删除平衡主要看兄弟节点，问问兄弟节点的孩子们，能不能借一个红色节点过来变成黑色。实在不行，这才去掉一层黑色节点，再向上询问。

对比红黑树与 AVL 树的删除平衡操作：

  • AVL 树的删除后平衡是与插入平衡相同的，因为违背的是同一个性质，所以调用相同的平衡操作。
  • 红黑树的删除平衡因为和插入平衡破坏的是不同的性质，所以需要不同的平衡操作来重新达到自平衡。

3. 最后

3.1 完整递归代码和测试

头文件：black_red_tree_recursive.h

cpp 文件：black_red_tree_recursive.cpp

*************************
After inserted, tree is:
pre order:
30(B) 10(B) 20(R) 60(R) 40(B) 50(R) 80(B) 70(R) 90(R)
mid order:
10(B) 20(R) 30(B) 40(B) 50(R) 60(R) 70(R) 80(B) 90(R)
*************************
remove value: 80 tree balance check : 1
remove value: 10 tree balance check : 1
remove value: 50 tree balance check : 1
remove value: 40 tree balance check : 1
*************************
After removed, tree is:
pre order:
30(B) 20(B) 70(R) 60(B) 90(B)
mid order:
20(B) 30(B) 60(B) 70(R) 90(B)

3.2 非递归完整代码

这里给出非递归的完整代码，主要区别在于增加了一个parent指针，使用while循环去遍历整个树，这一般才是会用在标准库的实现方式。因为效率要比递归方式更高。

头文件：black_red_tree.h

cpp 文件：black_red_tree.cpp

3.3 参考文档

知识共享许可协议
本文采用 CC A-NC-SA 4.0国际许可协议进行许可。
文章目录